What Do You Learn In 5th Grade Math
Even and Odd Functions
You may be asked to "determine algebraically" whether a function is even or odd. To do this, you take the function and plug –x in for ten , and then simplify. If you end upward with the exact same function that you started with (that is, if f(–x) = f(10), then all of the signs are the same), and then the function is fifty-fifty. If you lot end up with the exact opposite of what you started with (that is, if f(–x) = –f(x), so all of the signs are switched), so the function is odd.
In all other cases, the role is "neither even nor odd".
Let'southward see what this looks like in action:
Content Continues Beneath
-
Make up one's mind algebraically whether f(x) = –3x 2 + 4 is even, odd, or neither.
If I graph this, I will come across that this is "symmetric about the y -axis"; in other words, whatsoever the graph is doing on 1 side of the y -axis is mirrored on the other side:
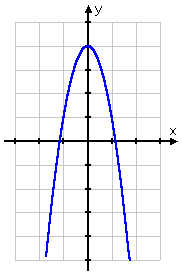
This mirroring about the y -centrality is a hallmark of even functions.
Also, I annotation that the exponents on all of the terms are even — the exponent on the constant term being zip: fourx 0 = 4 × i = 4. These are helpful clues that strongly suggest to me that I've got an even function here.
But the question asks me to make the conclusion algebraically, which means that I need to do the algebra.
So I'll plug –10 in for x , and simplify:
I can see, by comparing the original part with my final result above, that I've got a lucifer, which means that:
f(10) is even
-
Determine algebraically whether f(10) = 2x 3 – 4x is even, odd, or neither.
If I graph this, I volition encounter that information technology is "symmetric virtually the origin"; that is, if I beginning at a point on the graph on one side of the y -axis, and depict a line from that point through the origin and extending the same length on the other side of the y -axis, I will get to some other point on the graph.
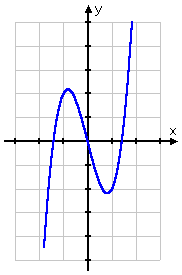
You tin too call up of this every bit the half of the graph on one side of the y -centrality is the upside-downwardly version of the half of the graph on the other side of the y -axis. This symmetry is a authentication of odd functions.
Annotation also that all the exponents in the function'south rule are odd, since the second term tin be written as fourx = 4x ane . This is a useful clue. I should expect this office to be odd.
The question asks me to make the determination algebraically, and then I'll plug –x in for x , and simplify:
f(–10) = ii(–x)3 – four(–10)
= 2(–x 3) + 4ten
= –twoten 3 + ivx
For the given function to be odd, I need the in a higher place result to have all reverse signs from the original role. And so I'll write the original office, and then switch all the signs:
original: f(ten) = 2(x)3 – 4(10)
switched: – f(x) = – 2x 3 + 4ten
Comparison this to what I got, I see that they're a lucifer. When I plugged –10 in for 10 , all the signs switched. This means that, as I'd expected:
f(x) is odd.
-
Determine algebraically whether f(ten) = 2ten iii – 3x 2 – 4ten + 4 is even, odd, or neither.
This function is the sum of the previous two functions. But, while the sum of an odd and an fifty-fifty number is an odd number, I cannot conclude the same of the sum of an odd and an fifty-fifty function.
Note that the graph of this function does not take the symmetry of either of the previous ones:
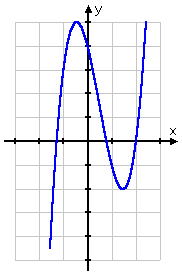
...nor are all of its exponents either even or odd.
Based on the exponents, likewise as the graph, I would expect this role to exist neither even nor odd. To be sure, though (and in lodge to get full credit for my answer), I'll demand to do the algebra.
I'll plug –x in for 10 , and simplify:
f(–x) = 2(–x)3 – 3(–x)2 – iv(–10) + iv
= ii(–x 3) – iii(10 two) + 4x + iv
= –2x 3 – 310 2 + 4x + 4
I tin see, past a quick comparison, that this does not lucifer what I'd started with, and then this function is not even. What about odd?
To bank check, I'll write down the exact reverse of what I started with, being the original function, but with all of the signs changed:
– f(x) = – 2x 3 + threex two + 4ten – 4
This doesn't match what I came up with, either. So the original function isn't odd, either. Then, as I'd expected:
f(ten) is neither even nor odd.
As y'all can encounter, the sum or difference of an even and an odd part is not an odd function. In fact, yous'll observe that the sum or departure of two fifty-fifty functions is some other fifty-fifty function, but the sum or departure of two odd functions is another odd part.
There is (exactly) i part that is both fifty-fifty and odd; information technology is the zero function, f(10) = 0.
In other words, "even" and "odd", in the context of functions, hateful something every unlike from how these terms are used with whole numbers. Don't try to mix the two sets of definitions; it'll only confuse you.
Merely because all of the examples so far have involved polynomial functions, don't recall that the concept of even and odd functions is restricted to polynomials. It'southward non. Trigonometry is full of functions that are even or odd, and other types of functions can come up under consideration, too.
-
Determine whether is even, odd, or neither.
This is a rational part. The process for checking if information technology'south even, odd, or neither is the same as always. I'll outset by plugging –x in for ten :
I can run across, by comparison, that this is the same as what I'd started with. And then:
g(x) is fifty-fifty
You may find it helpful, when answering this "fifty-fifty or odd" type of question, to write down –f(x) explicitly, and then compare this to any you get for f(–x). This can assistance yous make a confident determination of the correct answer.
Source: https://www.purplemath.com/modules/fcnnot3.htm
Posted by: clapperhavers.blogspot.com


0 Response to "What Do You Learn In 5th Grade Math"
Post a Comment